√画像をダウンロード odds versus odds ratio 163416-Odds vs odds ratio vs probability

 Odds ratios work the same An odds ratio of 108 will give you an 8% increase in the odds at any value of X Likewise, the difference in the probability (or the odds) depends on the value of X So if you do decide to report the increase in probability at different values of X, you'll have to do it at low, medium, and high values of X Odds ratio in this example is found to be hight () (P The difference between cats and dogs is 3 percentage points or 3 49 ≈ 612 % increase in probability for dogs over cats Meanwhile the odds ratio is 052 1 − 052 049 1 − 049 ≈ 1128 However I am finding a lot of social science literature intpreting O R − 1 as equivalent to increase in probability Example

Statistc 111 Lecture Notes Spring 19 Lecture 11 Odds Ratio Relative Risk Ert2

Odds vs odds ratio vs probability

Odds vs odds ratio vs probability-StATS Odds ratio versus relative risk (created by ) Dear Professor Mean There is some confusion about the use of the odds ratio versus the relative risk Can you explain the difference between these two numbers? Hazard ratio vs odds ratio interpretationAn odds ratio greater than 1 indicates that the condition or event is more likely to occur in the first group And an odds ratio less than 1 indicates that the condition or event is less likely to occur in the first group The odds ratio must be nonnegative if it is defined It is undefined if p 2 q 1

Adjusted Odds Ratios For Age And Sex 95 Confidence Intervals Of Download Table

 On the other hand, a gambler backing Manchester United, who have odds of 1/5, will see a payout of just $1 for every $5 bet That means a total payout of $6 for someone betting $5 Bournemouth 5/1 Manchester United 1/5 You Bet $ on Bournemouth You Win $100 ( x 5=100) You also get your $ bet backThe odds aren't as odd as you might think, and the log of the odds is even simpler!RELATIVE RISK AND ODDS RATIO An RR (or OR) more than 10 indicates an increase in risk (or odds) among the exposed compared to the unexposed, whereas a RR (or OR)

 e x p ( β) = odds ratio = p 1 1 − p 1 p 2 1 − p 2 I guess what's not coming across is how β, not being a ratio of odds, converts to the odds ratio metric, when taken out of logarithmic space To provide a bit more, if this is the logistic regression equation for the constant l o g ( p 1 − p) = β β 1 ∗ 0 β 2 ∗ 0 β 3 ∗ 0When the disease is rare, the odds ratio will be a very good approximation of the relative risk The more common the disease, the larger is the gap between odds ratio and relative risk In our example above, p wine and p no_wine were 0009 and 0012 respectively, so the odds ratio was a good approximation of the relative risk OR = 0752 and RR If the odds in favor of an event is known, the probability is just the odds divided by one plus the odds ie Probability= Odds/ (1Odds) What is the difference between Probability and Odds?

 The Rcode above demonstrates that the exponetiated beta coefficient of a logistic regression is the same as the odds ratio and thus can be interpreted as the change of the odds ratio when we increase the predictor variable \(x\) by one unit In this example the odds ratio"Odds" and "Risk" are the most common terms which are used as measures of association between variables In this article, which is the fourth in the series of common pitfalls in statistical analysis, we explain the meaning of risk and odds and the difference between the twoIn health care it is the ratio of the number of people with the event to the number without It is commonly expressed as a ratio of two integers For example, an odds of 001 is often written as 1100, odds of 033 as 13, and odds of 3 as 31

Epidemiology Stepwards

Plos One Biomarkers Of Host Response Predict Primary End Point Radiological Pneumonia In Tanzanian Children With Clinical Pneumonia A Prospective Cohort Study

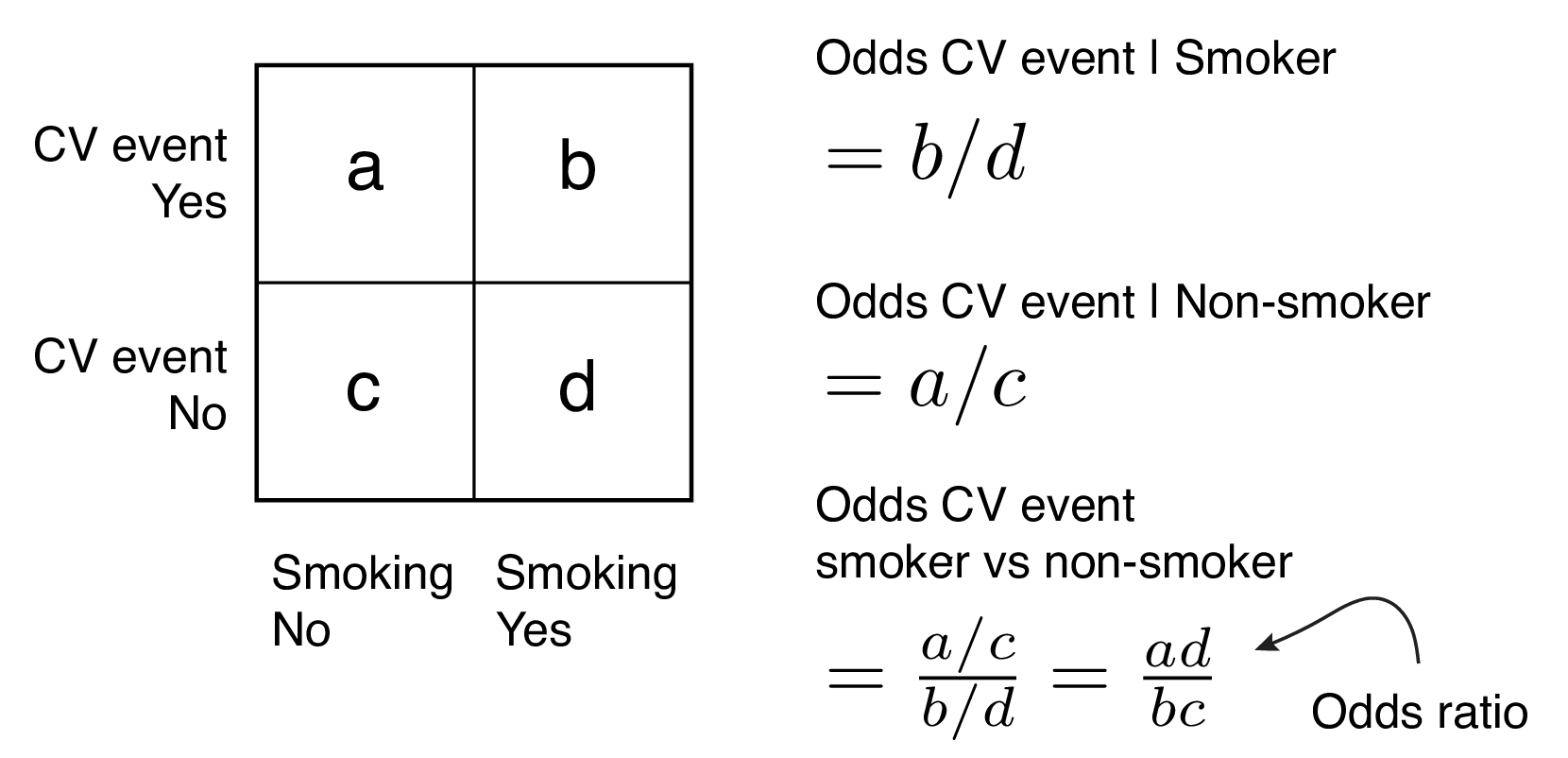
It is called that because it is the ratio of two odds Some people call the odds the odds ratio because the odds itself is a ratio That is fine English, but this can quickly lead to confusion If you did that, you would have to call this calculation the odds ratio ratio or the ratio of the odds ratios The odds ratio is the ratio of two odds ODDS RATIO Odds Ratio = Odds of Event A / Odds of Event B For example, we could calculate the odds ratio between picking a red ball and a green ball The probability of picking a red ball is 4/5 = 08 The odds of picking a red ball are (08) / 1(08) = 08 / 02 = 4 The odds ratio for picking a red This is called the odds ratio;

Forest Plot Showing The Pooled Odds Ratio Or Or Hazard Ratio Hr Of Download Scientific Diagram

Logit Wikipedia

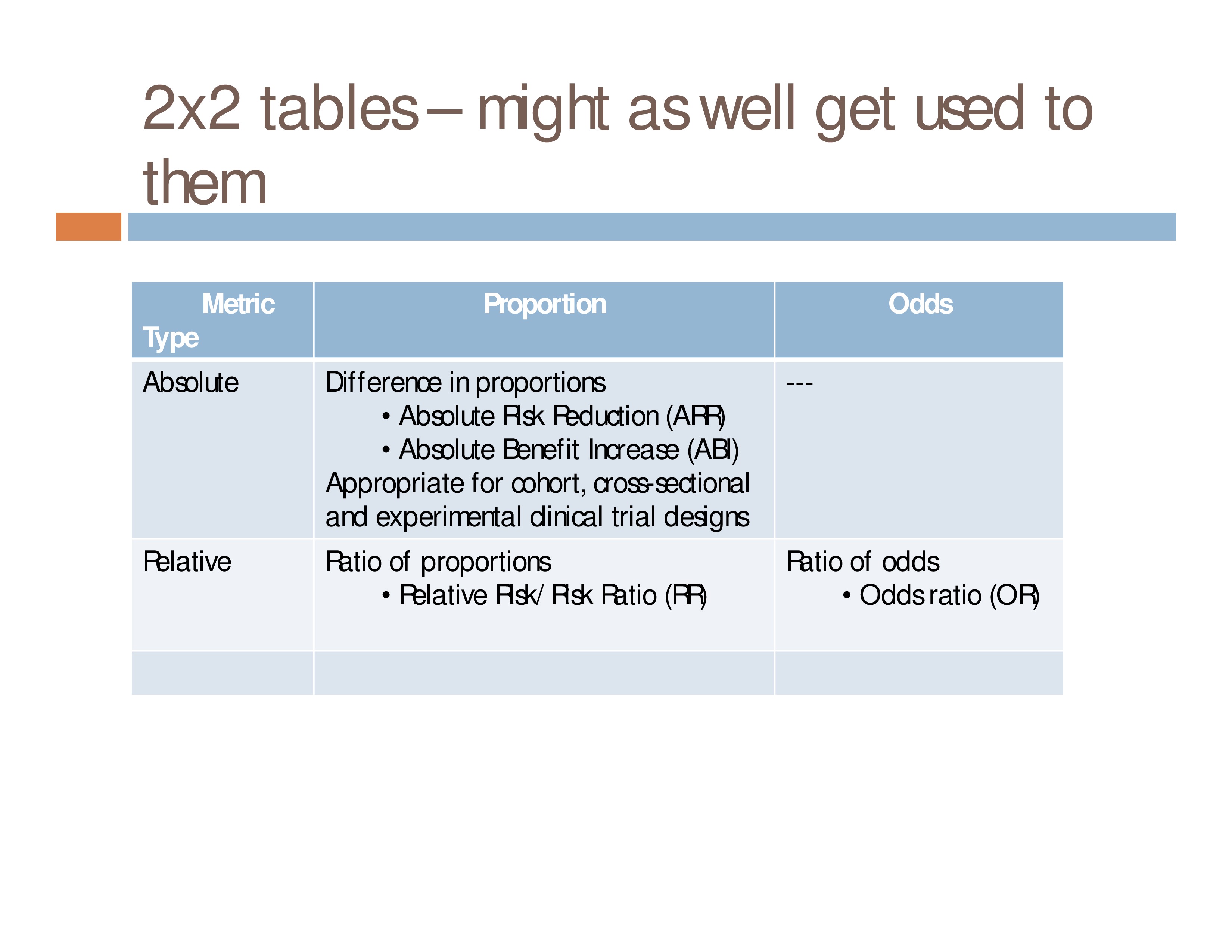
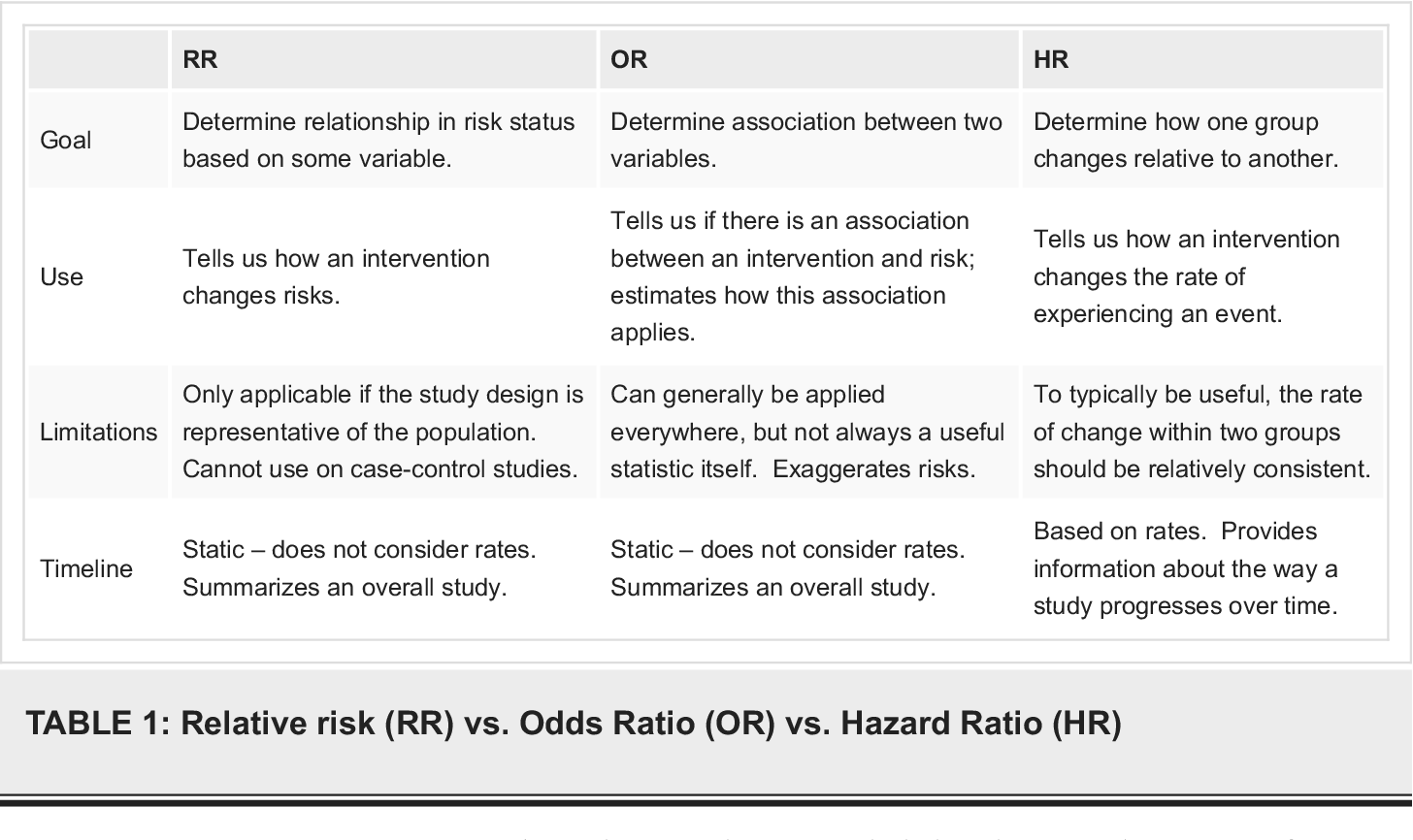
 Risk ratios, odds ratios, and hazard ratios are three ubiquitous statistical measures in clinical research, yet are often misused or misunderstood in their interpretation of a study's results A 01 paper looking at the use of odds ratios in obstetrics and gynecology research reported 26% of studies (N = 151) misinterpreted odds ratios as risk ratios , while a 12 paper INTRODUCTION Odds ratio (OR) and risk ratio (RR) are two commonly used measures of association reported in research studies In crosssectional studies, the odds ratio is also referred to as the prevalence odds ratio (POR) when prevalent cases are included, and, instead of the RR, the prevalence ratio (PR) is calculatedOdds ratio vs relative risk Odds ratios and relative risks are interpreted in much the same way and if and are much less than and then the odds ratio will be almost the same as the relative risk In some sense the relative risk is a more intuitive measure of effect size Note that the choice is only for prospective studies were the distinctionThe hazard ratio

Odds Vs Probabilities Odds Ratio In Spss Exp B Is An Odds Rather Than A Probability Odds Success Failure Probability Likelihood Of Success For Ppt Download

Forest Plot Of Odds Ratio For The Association Of Family History Of Dm And Hdp In Ethiopia

 Smoking The adjusted odds ratio for smoking is calculated as e485 = 1624 This means the odds of having a baby with low birthweight are increased by 624% if the mother smokes (compared to not smoking), assuming the variable age is held constant For example, suppose mother A and mother B are both 30 years oldFractional odds are the ratio of the amount (profit) won to the stake; An Odds Ratio (OR) then is simply the comparison of two odds, OR=Odds (A)/Odds (B) The Relative Risk (RR) is simply the comparison of two risks or probabilities, RR=Probability (A)/Probability (B) This is made more clear when the term is referred to as the Risk Ratio Let's look at this graphically

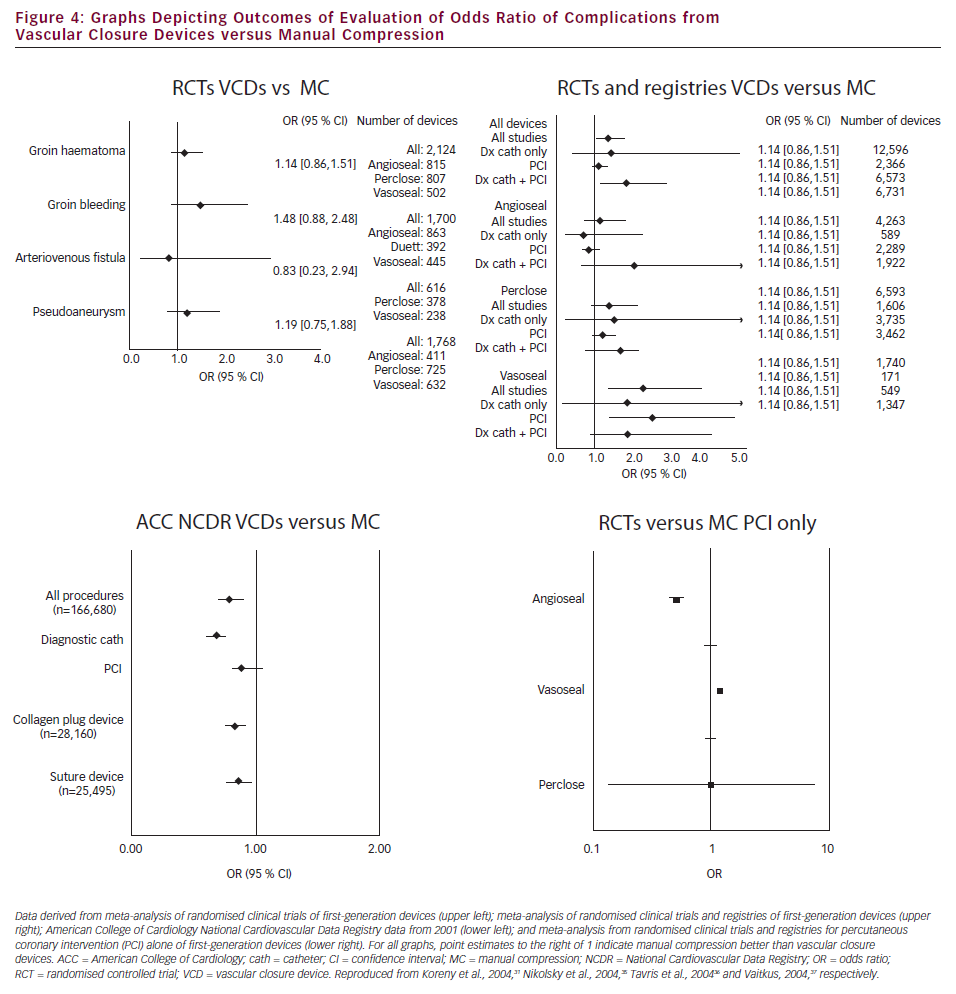
Graphs Depicting Outcomes Of Evaluation Of Odds Ratio Of Complications From Vascular Closure Devices Versus Manual Compression Ecr Journal

Www Jstor Org Stable

Odds Ratios and Log(Odds Ratios) are like RSquared they describe a relationship between two things And just like RSquared, you need to determine if this When the Odds ratio is above 1 and below 2, the likelihood of having the event is represented as XX % higher odds (where XX % is Odds ratio 1) That means that if odds ratio is 124, the likelihood of having the outcome is 24% higher (124 – 1 = 024 ie 24%) than the comparison groupThe odds ratio is defined as the ratio of the odds of an event or disease occurring in one group to the odds occurring in another group The standard formula is X / ( 1 − X) / Y / ( 1 − Y), where X and Y are the probability of that event in the two groups, respectively In contrast, the relative risk is the risk of an event or disease

Ppt Odds Ratio Vs Relative Risk Powerpoint Presentation Free Download Id

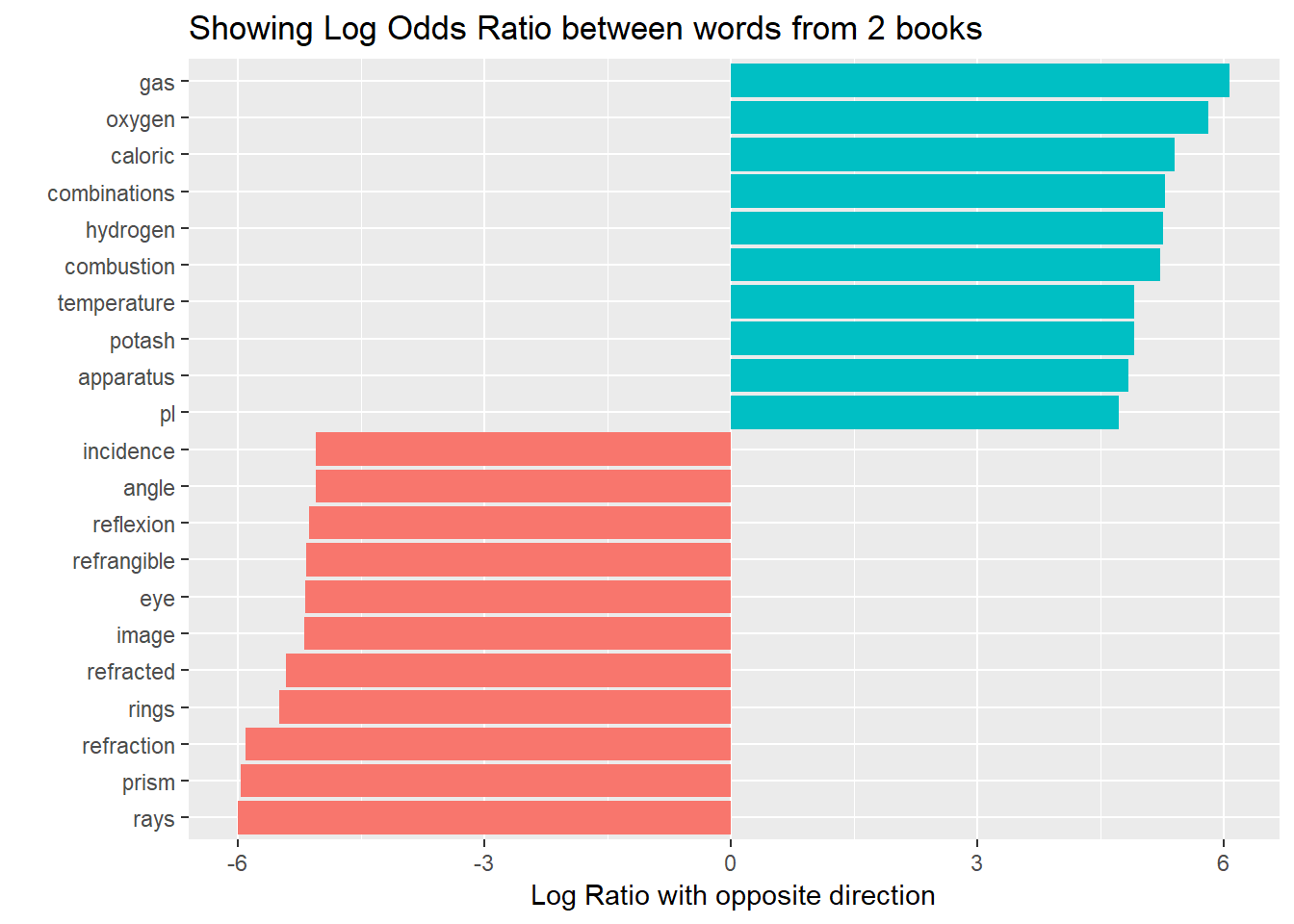
Log Odds Ratio Vs Tf Idf Vs Weighted Log Odds

• Probability is expressed as a number between 0 and 1, while Odds is expressed as a ratio • Probability ensures that an event will occur, but OddsDecimal odds represent the amount one wins for every $1 wagered American odds, depending on the negative or In mathematics, the term odds can be defined as the ratio of number of favourable events to the number of unfavourable events While odds for an event indicates the probability that the event will occur, whereas odds against will reflect the likelihood of nonoccurrence of the event

Answered Ert Format Tools Table Window Help 53 Bartleby

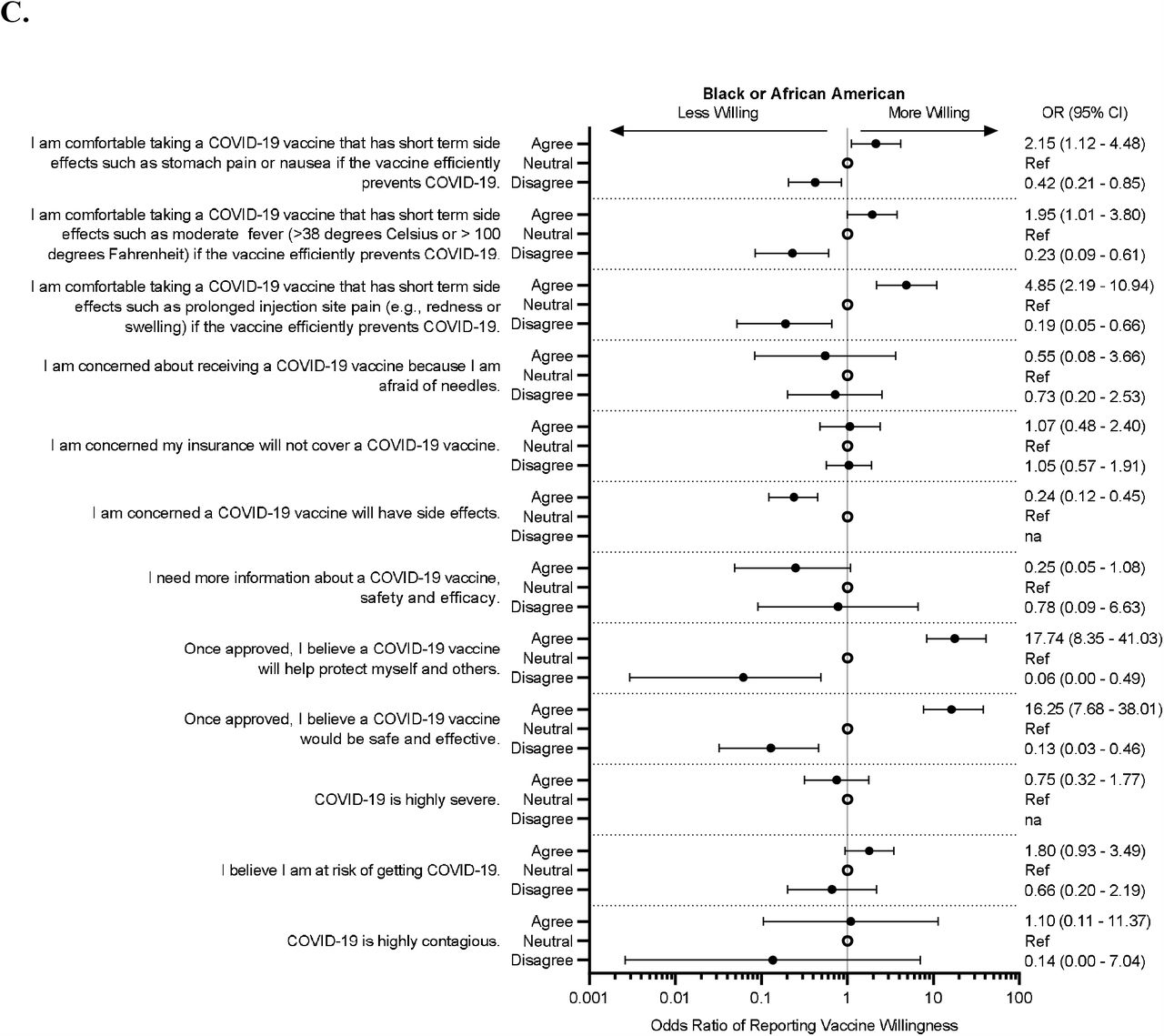
Factors Indicating Intention To Vaccinate With A Covid 19 Vaccine Among Older U S Adults Medrxiv

Ratio Pot Odds / Ratio It is not just number from percentage but it is upside down pot size amount you have to call pot was $80 and they bet $ $100 pot and call $ = 5 1 You are risking $1 to win $5 Now the pot is $1 Hand Odds (cards left outs)/outs If you have 8 outs on the turn then (468)/8 = 475 1 or (1 fraction Definition The Odds Ratio is a measure of association which compares the odds of disease of those exposed to the odds of disease those unexposed Formulae OR = (odds of disease in exposed) / (odds of disease in the nonexposed) Example I often think food poisoning is a good scenario to consider when interpretting ORs Imagine a group of friends went out to A highly simplified example illustrates this Suppose that 18 out of patients (90 percent probability, odds of 91) in an experiment lost weight while using diet A, while 16 out of (80 percent, odds of 41) lost weight using diet B The relative risk of losing weight by choosing diet A over diet B is 1125, while the odds ratio is about 225

Gout Attack Odds Ratio Versus Alcohol Consumed Imgur

Experimental Designs For Robust Detection Of Effects In Genome Wide Case Control Studies Genetics

In terms of odds ratios, we can say that for male students, the odds ratio is exp (13) = 114 for a oneunit increase in math score and the odds ratio for female students is exp (197) = 122 for a oneunit increase in math score odds ratios approximate relative risk ratios, when the outcomes are not rare, odds ratios always overestimate relative risk ratios, a problem that becomes more acute as the baseline prevalence of the outcome exceeds 10% Odds ratios cannot be calculated directly from relative risk ratios For example, an odds ratio for The difference between odds ratio and risk ratio While Risk Ratio is the probability of one thing divided by the probability of another (usually in a separated group), Odds Ratio is the odds of one event happening divided by the odds of another EssoeOdds1

9 2 Binary Logistic Regression R For Health Data Science

Event Based Measures Of Effect Size Asha Journals Academy

Odds ratios (OR) are commonly reported in the medical literature as the measure of association between exposure and outcome However, it is relative risk that people more intuitively understand as a measure of association Relative risk can be directly determined in a cohort study by calculating a risk ratio (RR)An odds ratio of 112 means the odds of having eaten lettuce were 11 times higher among casepatients than controls Because the odds ratio is greater than 10, lettuce might be a risk factor for illness after the luncheon The magnitude of the odds ratio suggests a strong association The odds ratio is extremely important, however, as it is the only measure of effect that can be computed in a casecontrol study design When the outcome of interest is relatively rare (

Absolute Risk Vs Relative Risk Vs Odds Ratio Pp Made Easy On Vimeo

Forest Plot Of The Odds Ratio With Corresponding 95 Confidence Intervals For H Pylori Infection On Obese Subjects Versus Normal Weight Subjects

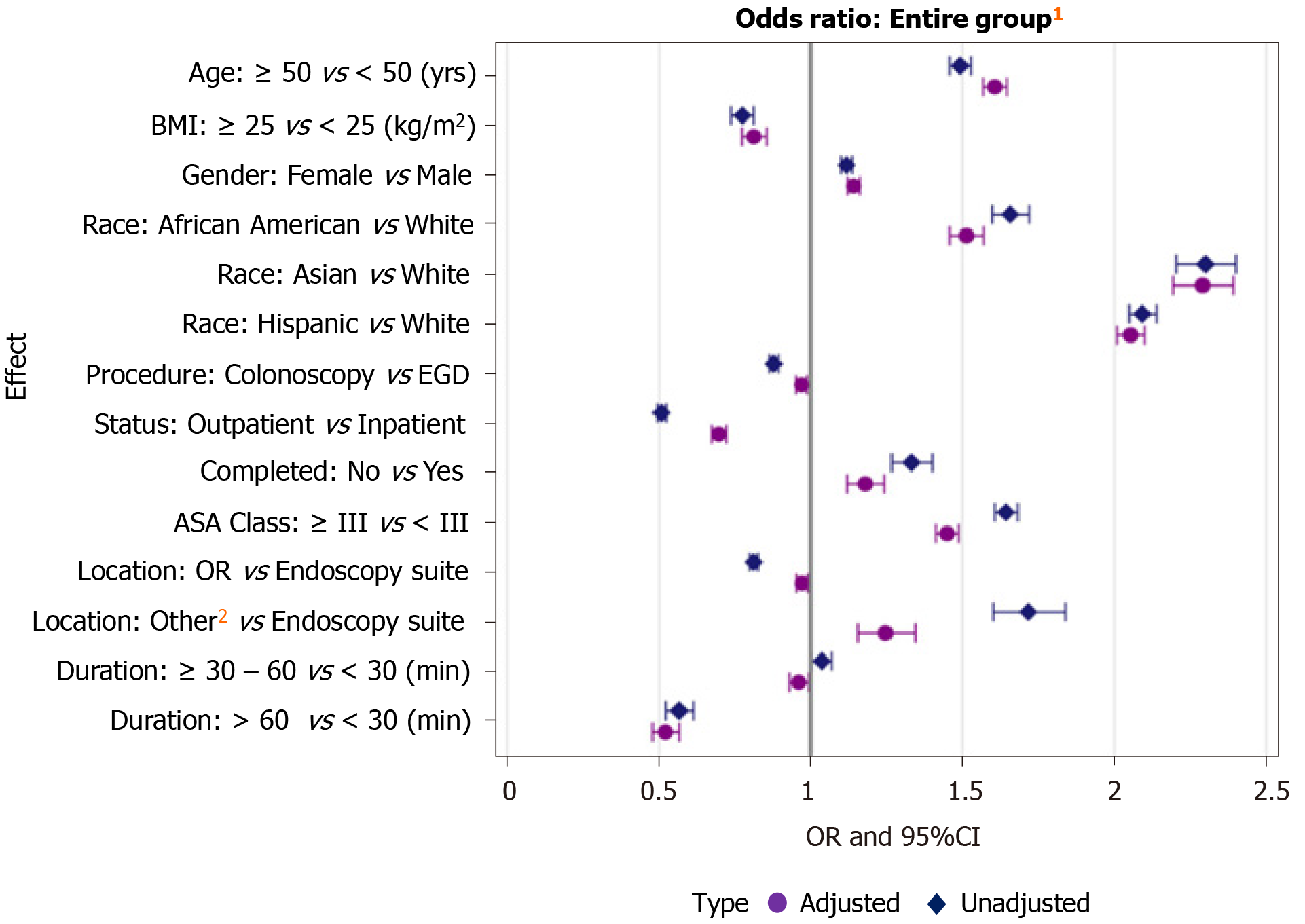
 Odds are the ratio of something happening to something not happening In our scenario above, the odds are 4 to 6 Whereas, Probability is the ratio of something happening to everything that could happen So in the case of our chess example, probability is 4 to 10 (as there were 10 games played in total)Both the odds ratio and the relative risk compare the likelihood of an event between two groups Like we did with the risk, we can calculate the ratio of the odds of the two groups to get the odds ratio (OR), which gives us an idea of how much more likely is the event to occur in one group than the other As you can see, they are similar but different concepts In both cases, the null value is one

Impact Of An Electronic Health Record Ehr Reminder On Human Papillomavirus Hpv Vaccine Initiation And Timely Completion American Board Of Family Medicine

Statquest Odds Ratios And Log Odds Ratios Clearly Explained Youtube

 The odds ratio (OR) is a measure of how strongly an event is associated with exposure The odds ratio is a ratio of two sets of odds the odds of the event occurring in an exposed group versus the odds of the event occurring in a nonexposed group Odds ratios commonly are used to report casecontrol studies The odds ratio helps identify how likely an Odds seems less intuitive It is the ratio of the probability a thing will happen over the probability it won't In the spades example, the probability of drawing a spade is 025 The probability of not drawing a spade is 1 025 Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds for it happening are 075/025 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 against

Odds Ratio Relative Risk Risk Difference Statistics Tutorial 30 Marinstatslectures Youtube

Relationship Between Frailty And Mortality Hospitalization And Cardiovascular Diseases In Diabetes A Systematic Review And Meta Analysis Cardiovascular Diabetology Full Text

 The basic difference is that the odds ratio is a ratio of two odds (yep, it's that obvious) whereas the relative risk is a ratio of two probabilities (The relative risk is also called the risk ratio) Let's look at an example Relative Risk/Risk Ratio Suppose you have a school that wants to test out a new tutoring program An odds ratio is a relative measure of effect, which allows the comparison of the intervention group of a study relative to the comparison or placebo group So when researchers calculate an odds ratio they do it like this The numerator is the odds in the intervention arm The denominator is the odds in the control or placebo arm = Odds Ratio (OR)This is called the odds ratio;

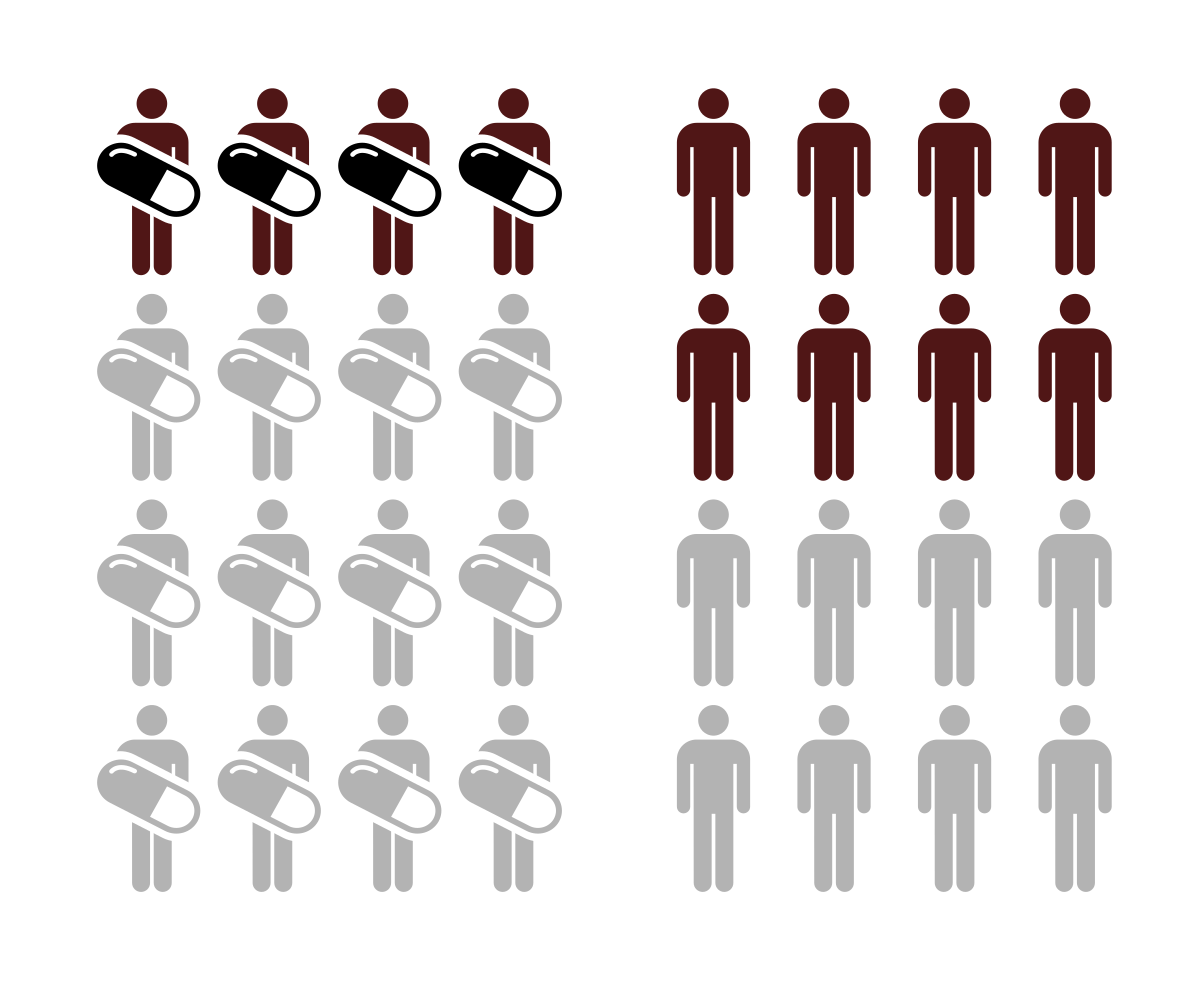
Epos Trade

Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios

This StatQuest covers those subjects so that you can understand the statiThe odds ratio is simply the ratio between the following two ratios The ratio between standard treatment and the new drug for those who died, and the ratio between standard treatment and the new drug for those who survived From the data in the table 1, it is calculated as follows OR = (a/b)/ (c/d) = (152/17)/ Odds ratio An odds ratio (OR) is another measure of association that quantifies the relationship between an exposure with two categories and health outcome Referring to the four cells in Table 315, the odds ratio is calculated as Odds ratio = (

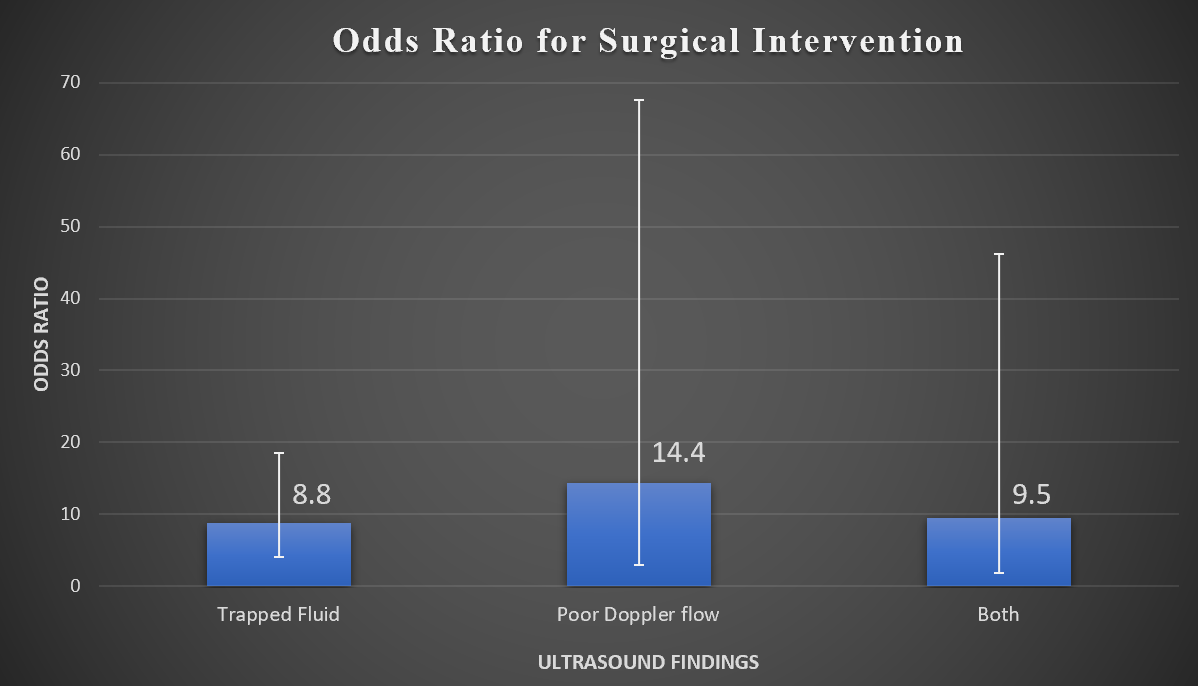
Risk Factors For The Development Of Acute Respiratory Distress Syndrome In Mechanically Ventilated Adults In Peru A Multicenter Observational Study Critical Care Full Text

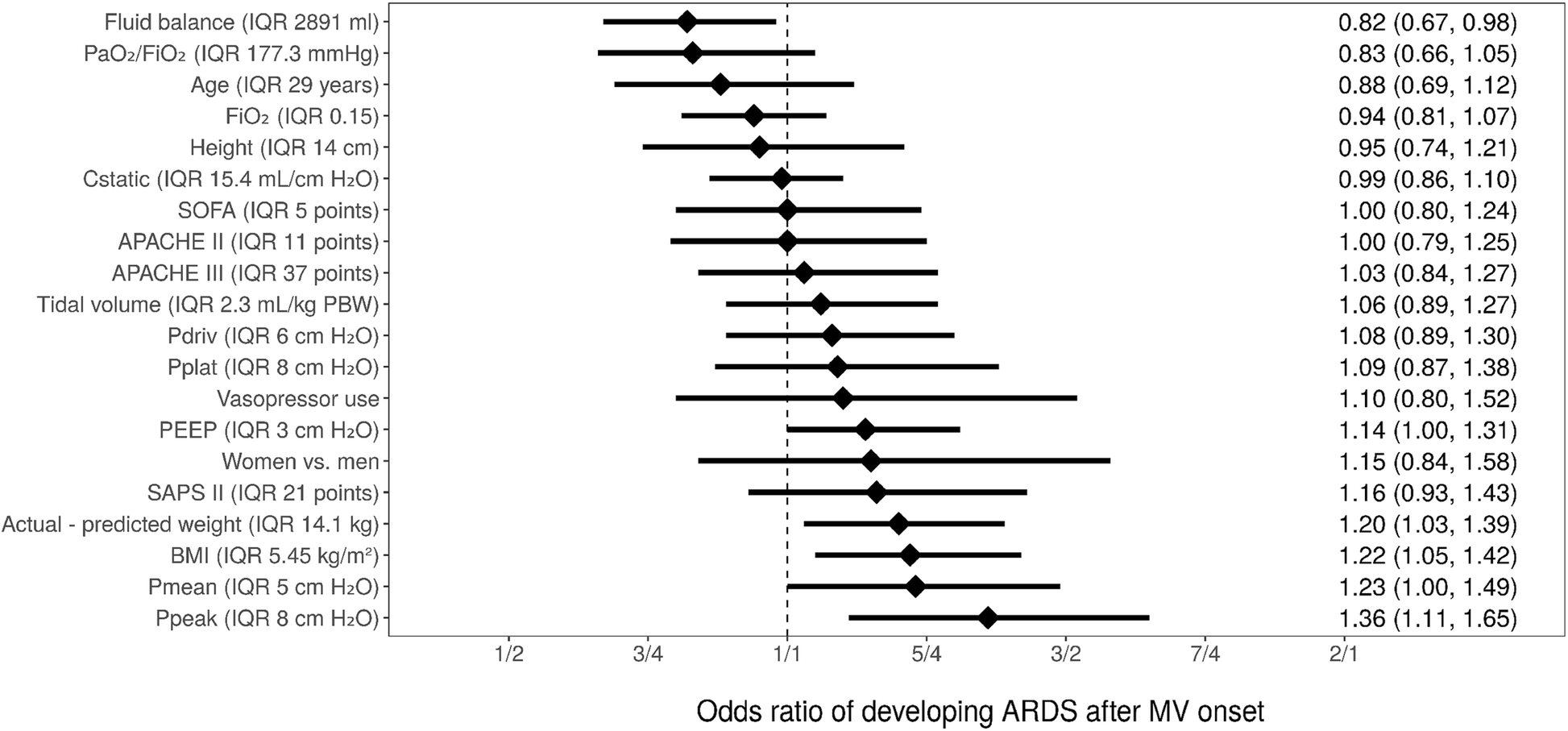
Bryan Carmody For M2s Preparing For Usmle Step 1 Epidemiology Questions Are Free Points You Don T Have To Make 2x2 Tables Or Memorize Formulae From First Aid To Calculate Or

In gambling, the odds describes the ratio of the size of the potential winnings to the gambling stake;

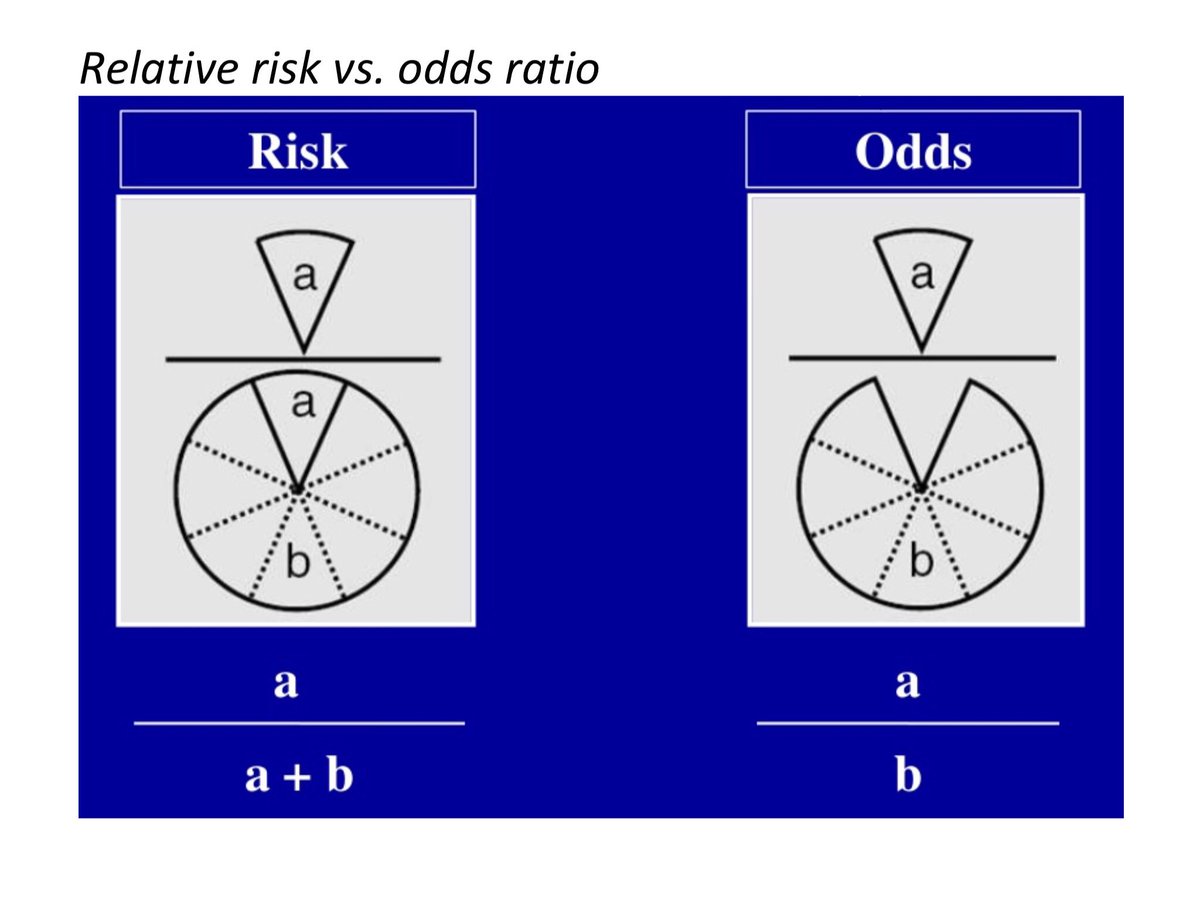
Relative Risk Wikipedia

View Image

Plos Neglected Tropical Diseases Snakebite Associated Thrombotic Microangiopathy A Systematic Review Of Clinical Features Outcomes And Evidence For Interventions Including Plasmapheresis

How To Calculate Odds Ratio And Relative Risk In Excel Statology

Odds Ratios Vs Risk Ratios Stats By Slough

2

When Can Odds Ratios Mislead The Bmj

Academic Oup Com Ije Article Pdf 26 1 2 2 Pdf

Odds Ratio Interpretation Confounder Diabetes Ppt Download

Relative Risk Odds Ratios Youtube

Ppt Relative Risk Increased Risk And Odds Ratios Powerpoint Presentation Id

Figure 5 Kidney Function Improvement Panel A And Worsening Panel B Ptras Versus Medical Therapy Alone Renal Artery Stenosis Management Strategies Ncbi Bookshelf

Www Researchsquare Com Article Rs 1069 V1 Pdf

Trtq08v 3 Lwm

What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science

View Image

Odds Ratio Relative Risk

2

Training Cochrane Org Handbook Statistical Methods Revman5

Part A Calculate The Odds Ratio Part B Calculate Chegg Com

2

Pdf What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios Semantic Scholar

1

What Is An Odds Ratio And How Do I Interpret It Critical Appraisal

Statistc 111 Lecture Notes Spring 19 Lecture 11 Odds Ratio Relative Risk Ert2

Solved Logistic Regression Modeling Outcomes 1 Vs 0 In Sas Support Communities

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

Ascpt Onlinelibrary Wiley Com Doi Pdf 10 1111 Cts

Odds Ratios Vs Risk Ratios Stats By Slough

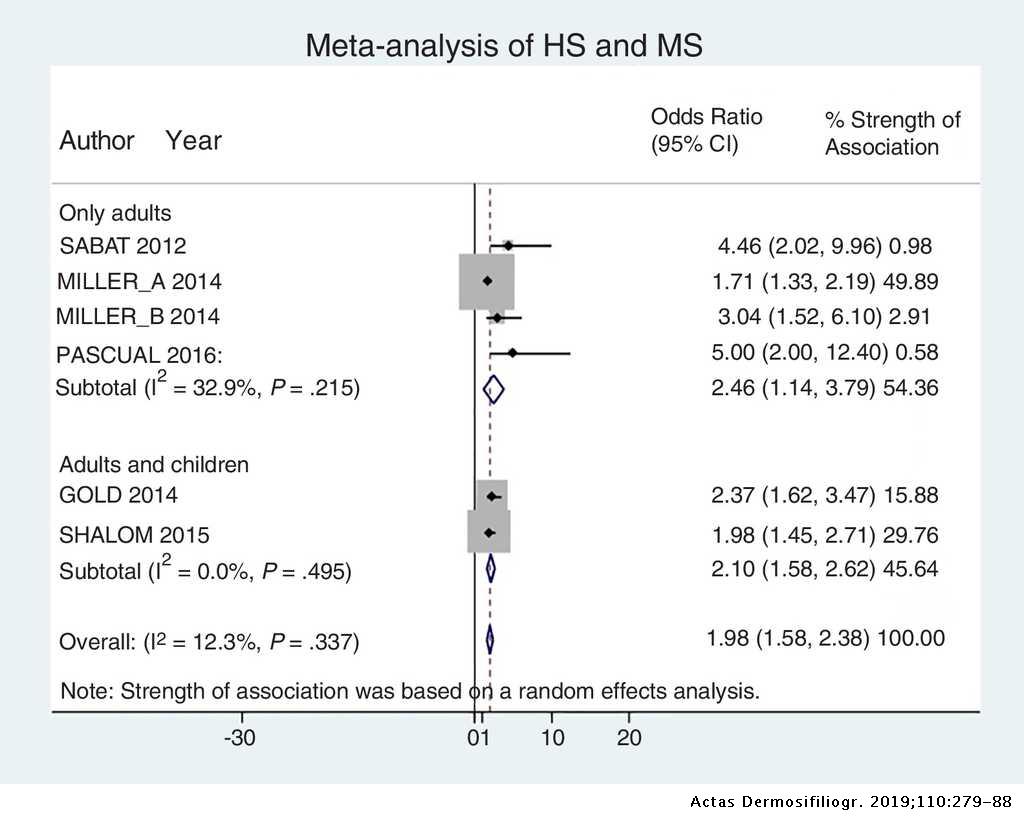
Association Between Hidradenitis Suppurativa And Metabolic Syndrome A Systematic Review And Meta Analysis Actas Dermo Sifiliograficas

The Math Behind Betting Odds Gambling

Adjusted Odds Ratios For Age And Sex 95 Confidence Intervals Of Download Table

View Image

Logistic Regression Kleinbaum 10 Flip Book Pages 451 500 Pubhtml5

1

Xmlinkhub

Q Tbn And9gcq5tpzikqe8jiy9iqzxyqcbaqndofe8d2iabvvrkarpadvgvm8o Usqp Cau

Re 999 999 Odds Ratio In Logistic Regression M Sas Support Communities

Experimental Designs For Robust Detection Of Effects In Genome Wide Case Control Studies Genetics

9 2 Binary Logistic Regression R For Health Data Science

Identifying Who Best Tolerates Moderate Sedation Results From A National Database Of Gastrointestinal Endoscopic Outcomes

Homework 2 Odds Ratio Vs Risk Ratio Exercise The Chegg Com

How Can We Convert Rate Ratio To Odds Ratio

Risk Factors For Severe Illness And Death In Covid 19 A Systematic Review And Meta Analysis Medrxiv

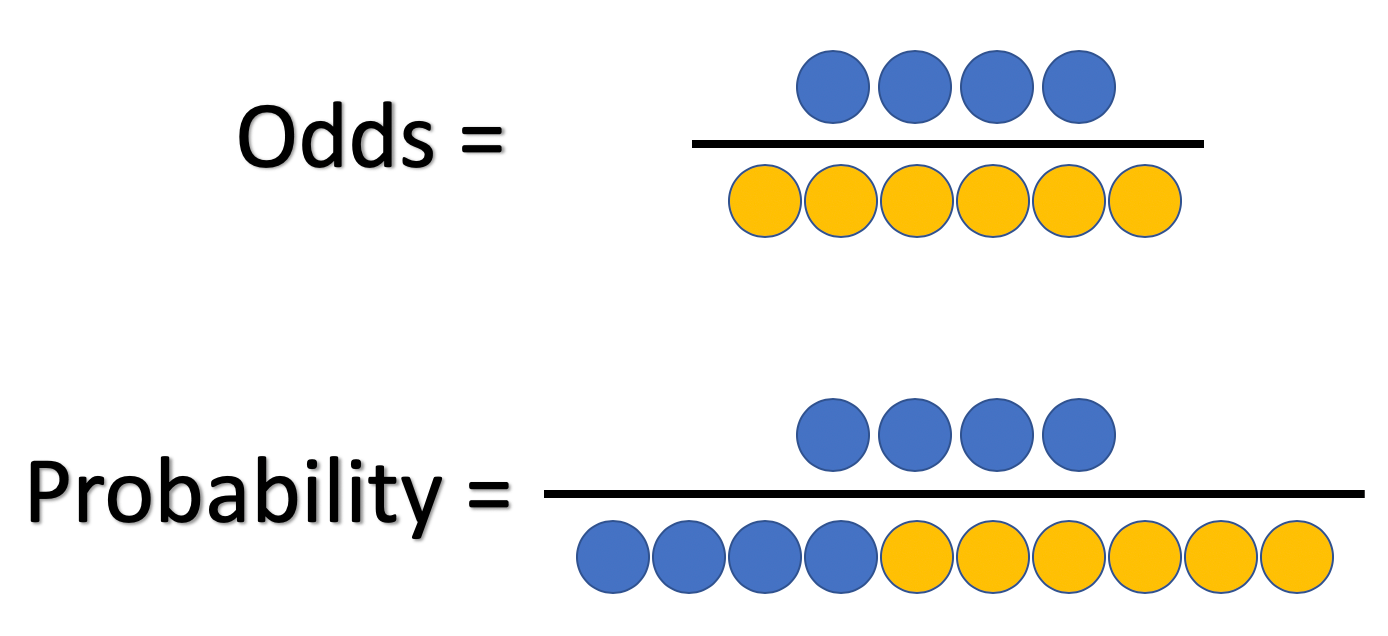
What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science

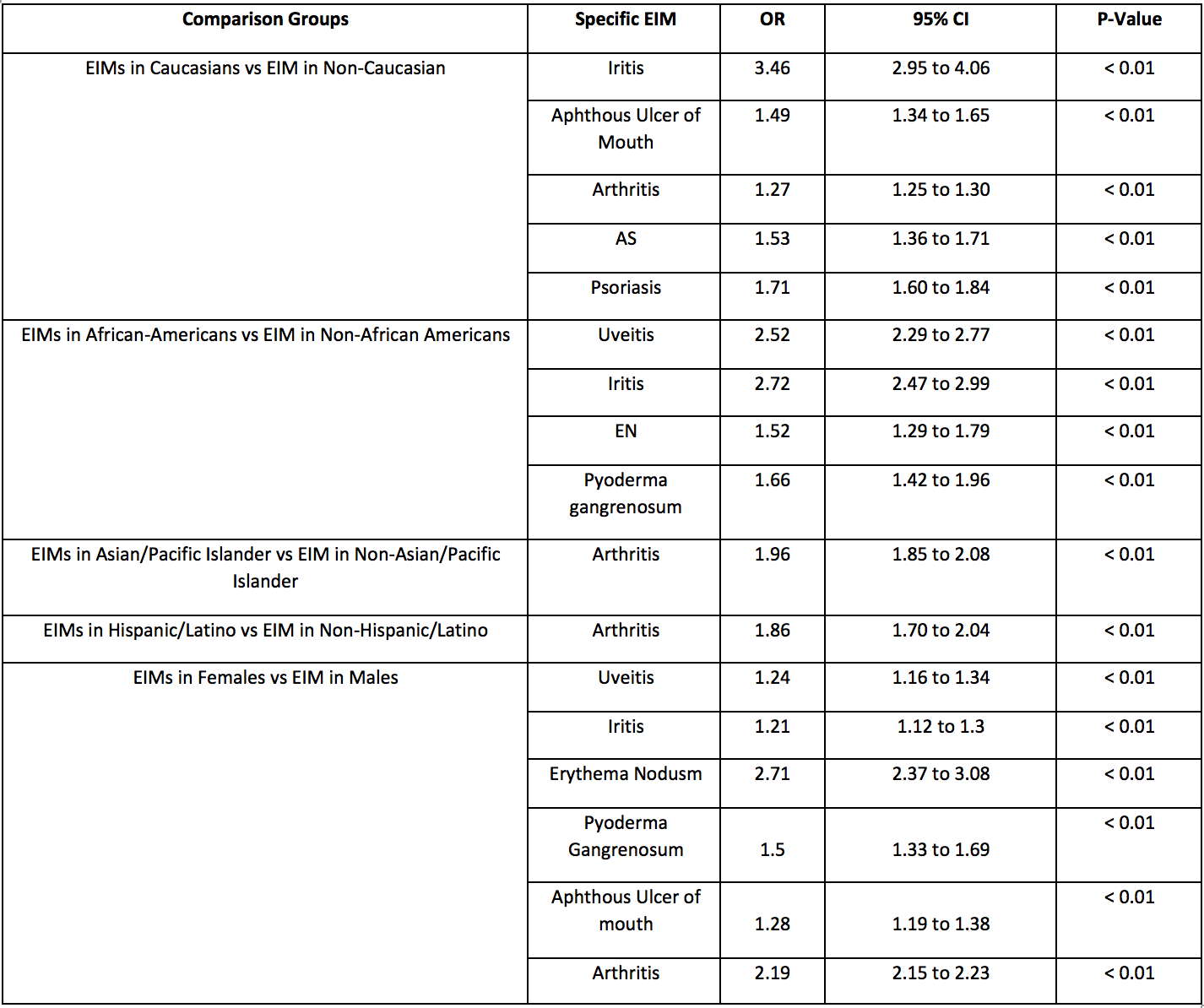
Acg Annual Meeting

Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios

Confidence Intervals For The Odds Ratio In Logistic Regression With Two Binary X S Pdf Confidence Interval Logistic Regression

2

Understanding Systematic Reviews And Meta Analysis Archives Of Disease In Childhood

Case Control Studies Statistics Ppt Download

Http Www Lexjansen Com Wuss 1999 Wuss Pdf

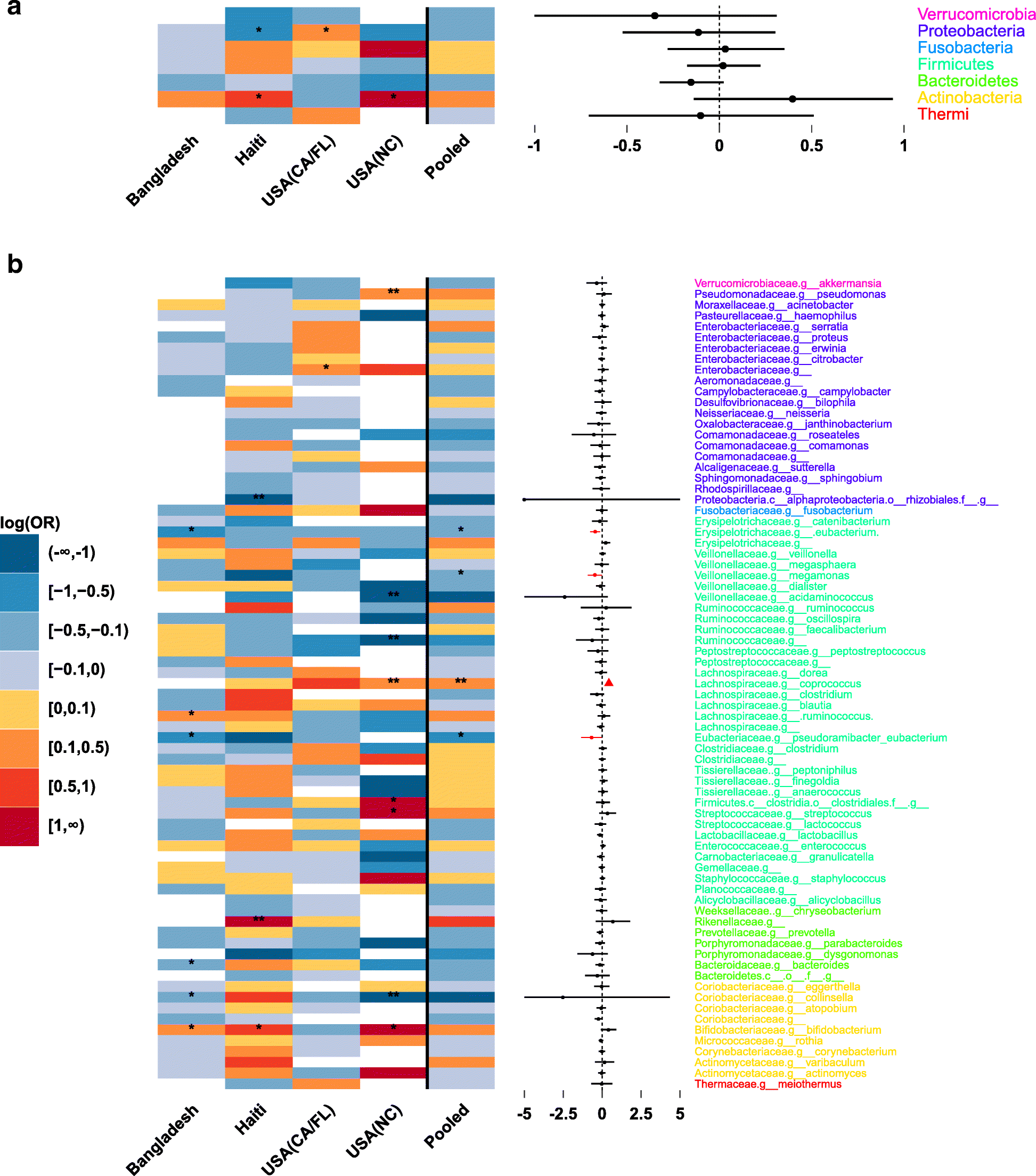
Metamicrobiomer An R Package For Analysis Of Microbiome Relative Abundance Data Using Zero Inflated Beta Gamlss And Meta Analysis Across Studies Using Random Effects Models Bmc Bioinformatics Full Text

Ascpt Onlinelibrary Wiley Com Doi Pdf 10 1111 Cts

Plot Of The Pooled Odds Ratio Of Psa Doubling Time 6 Vs 6 Months Download Scientific Diagram

Using Odds Ratio In Case Control Studies Youtube

1

Ppt The Odds Ratio Relative Odds Powerpoint Presentation Free Download Id 6056

Http Www Stat Colostate Edu Inmem Gumina St1 Class15 Downloads Oddsdratio Sol Example Pdf

Statquest Odds Ratios And Log Odds Ratios Clearly Explained Youtube

2

Evidencebased Journal Club Intentiontotreat Odds And Risk Paul

Forest Plots Of Relative Risks And Odds Ratios Of Detecting Fecal Download Scientific Diagram

Logistic Regression Circulation

Assessing Heterogeneity Of Treatment Effect Estimating Patient Specific Efficacy And Studying Variation In Odds Ratios Risk Ratios And Risk Differences Statistical Thinking

Table 4 Key Data On Odds Ratios

Slides Show

Figure 3 Associations Between Age At The Introduction Of Solid Foods And Allergic Sensitization To Wheat Allergen The Odds Ratios Were Adjusted For Season Of Birth Delivery Hospital Gender Number Of Siblings Parental Asthma Parental Allergic Rhinitis

2

Relative Risk Versus Odds Ratio Usmle Biostatistics 4 Youtube

Plos One Variability In The Effect Of 5 Httlpr On Depression In A Large European Population The Role Of Age Symptom Profile Type And Intensity Of Life Stressors

Effect Sizes Basicmedical Key

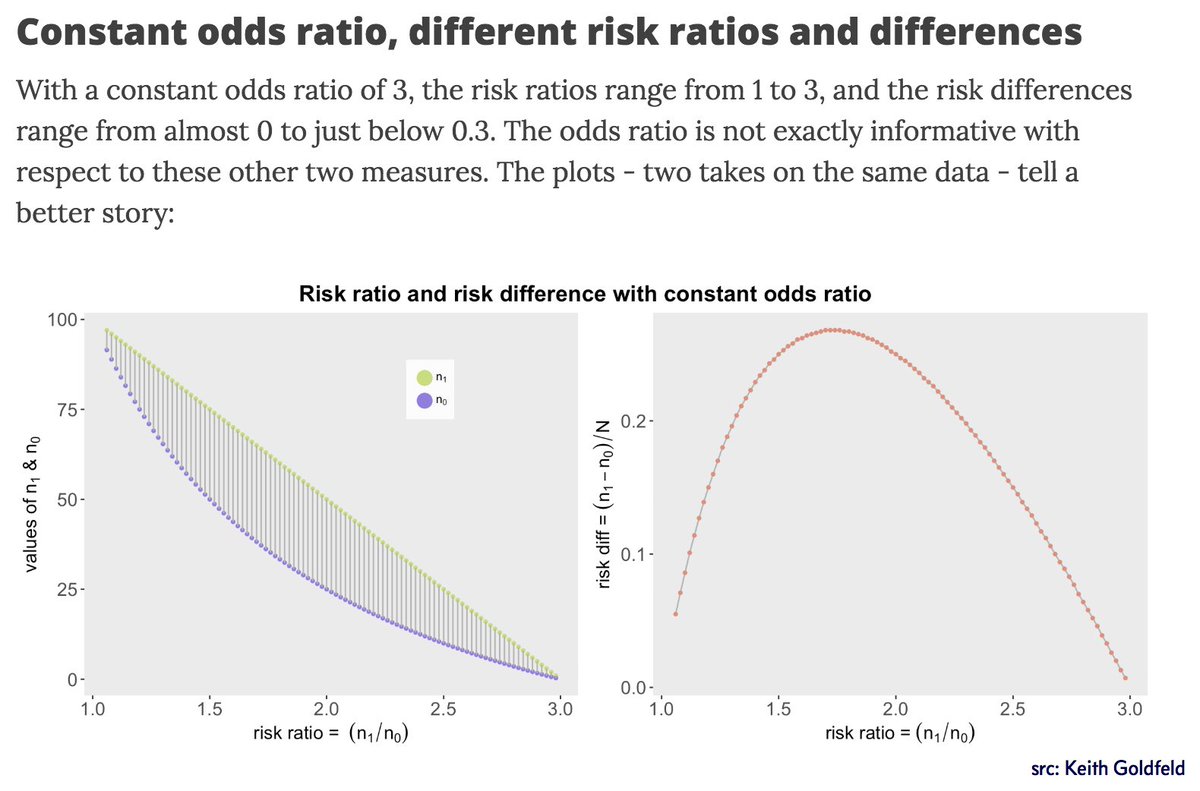
Mara Averick As Someone Who Asks For Odds Ratios And Relative Risk At The Vet I This Post How The Odds Ratio Confounds A Brief Study In A

Diagnostic Odds Ratio Wikipedia

Odds Ratios And Risk Ratios Youtube

Pdf A Limitation Of The Diagnostic Odds Ratio In Determining An Optimal Cut Off Value For A Continuous Diagnostic Test Semantic Scholar

Http U Demog Berkeley Edu Andrew Teaching Compare Prob Pdf

Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium

Incoming Term: odds versus odds ratio, odds versus risk ratio, log odds versus odds ratio, likelihood vs odds ratio, odds vs odds ratio vs probability, relative odds vs odds ratio, risk difference versus odds ratio, relative risk vs odds ratio when to use, relative risk vs. odds ratio logistic regression, absolute risk vs odds ratio,